Cálculo de Variaciones
Sistema
Considere el sistema:
x ̇(t) = f (x) + g(x)u(t), (1)
y (t) = x(t).
x(t0) = x0
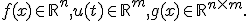
f(x)\in \mathbb{R}^{n}, u(t)\in \mathbb{R}^{m}, g(x)\in \mathbb{R}^{n\times m}.
Índice de Desempeño
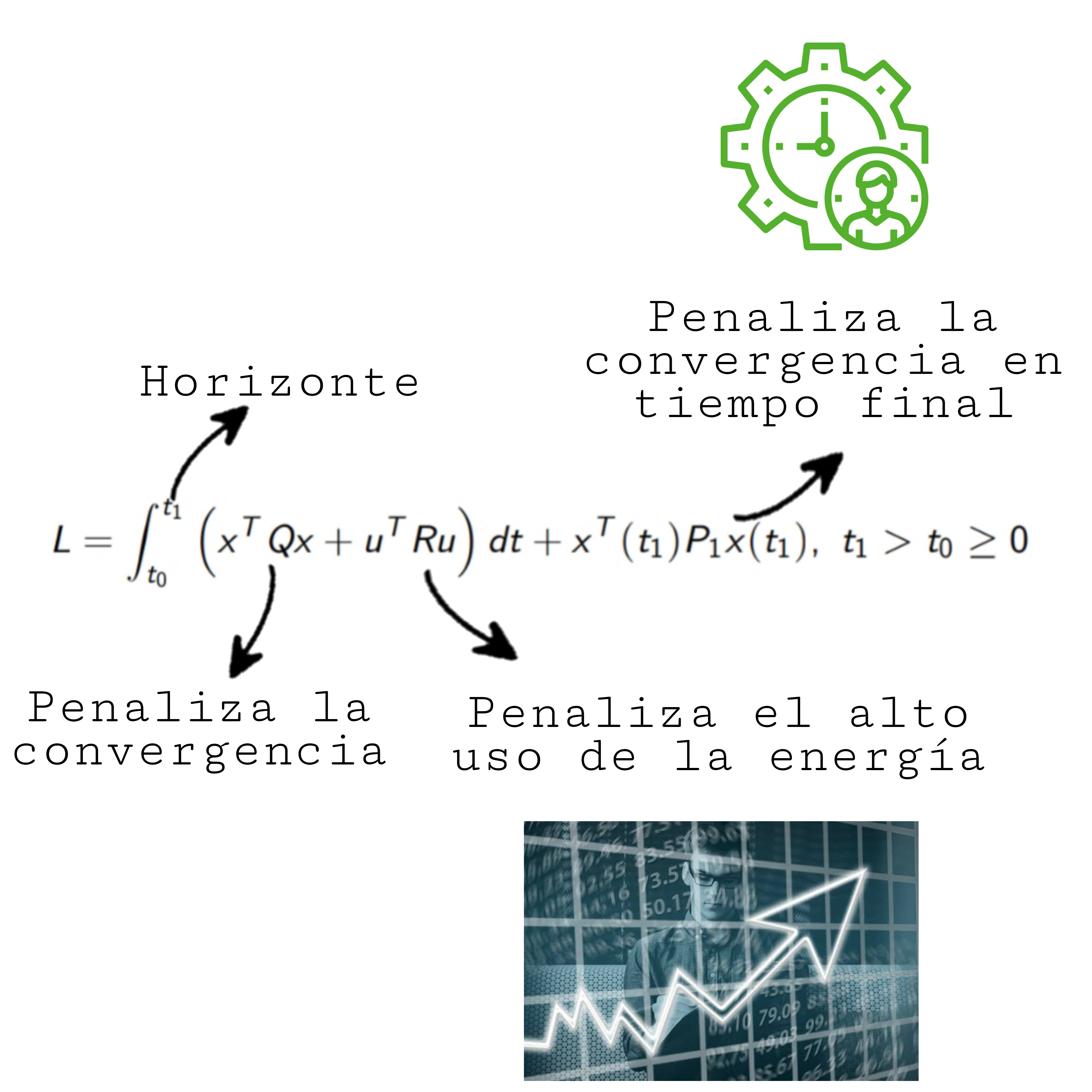
Defina el siguiente índice de desempeño:
Donde:
|
Donde:
Q,P_{1}\in \mathbb{R}^{n\times n} y R\in \mathbb{R}^{m\times m}, Q,P_{1}\geq 0, R>0 |
| Se supone que el estado es conocido y el sistema es completamente observable-controlable. |
|
Está función hace referencia a los a sistemas tales como:
|
|
Un índice de desempeño es una medida cuantitativa del desempeño de un sistema y se elige de manera que se dé énfasis a las especificaciones importantes del sistema. En otras palabras, este índice es un número que nos dice que tan «bueno» penaliza el uso.
|