Lema |
| Una condición necesaria sobre la segunda variación para tener un máximo local (u*es máximo local) es que |
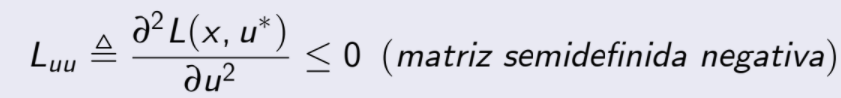 |
Prueba
Por contradicción (u* es máximo local pero ![]()
Proponga el control
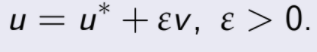
Sea ![]() como
como ![]() se tiene que
se tiene que
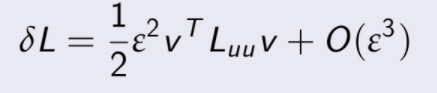
como ![]() depende de una potencia mayor que
depende de una potencia mayor que 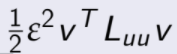
es posible elegir un ε suficientemente pequeño tal que 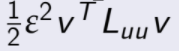 domine a
domine a ![]()
Prueba
Como supusimos que ![]() se tiene que
se tiene que ![]() por lo que
por lo que
![]()
lo que implica que
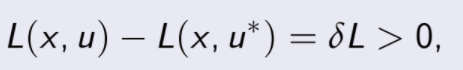
y consecuentemente se tiene que por lo que
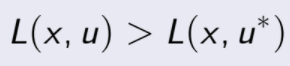
pero esto contradice el hecho de que u* es máximo local, por lo que ![]() , es decir algunos de sus valores propios podrían ser cero o negativos, pero nunca positivos.
, es decir algunos de sus valores propios podrían ser cero o negativos, pero nunca positivos.
- A esta condición se le llama segunda variación.
- Esto motiva resolver el problema mediante el CALCULO VARIACIONAL.