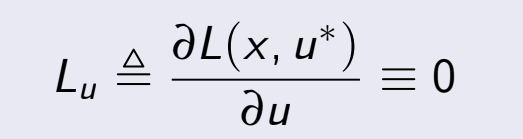LemaUna condición necesaria sobre la primera variación para tener un máximo
|
Prueba
Por contradicción. Suponemos que u* es máximo local, pero que ![]() . Se propone la siguiente ley de control.
. Se propone la siguiente ley de control.
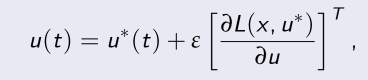
Donde ![]() puede ser elegida arbitrariamente pequeño. Sustituyendo
puede ser elegida arbitrariamente pequeño. Sustituyendo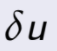 se
se
tiene que:
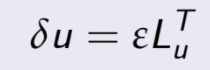
Sustituyendo el valor de ![]() en la serie de Taylor:
en la serie de Taylor:
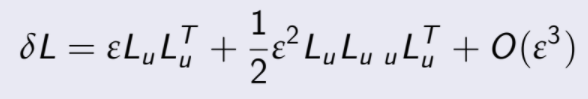
por lo que se tiene que
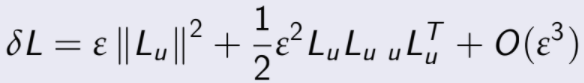
debido a que ![]() implica que existe un valor de ε suficientemente
implica que existe un valor de ε suficientemente
pequeño tal que el término ![]() (estrictamente positivo) domina en magnitud al segundo término
(estrictamente positivo) domina en magnitud al segundo término ![]() (observe que ε2 es mas pequeño que ε) por lo que
(observe que ε2 es mas pequeño que ε) por lo que
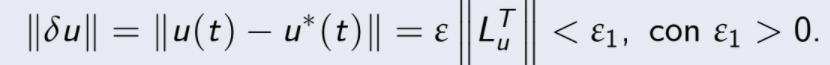
CONDICIÓN ESTACIONARIA.
Esto significa que para cualquier ε1 vecindad conteniendo a u existe un control u tal que
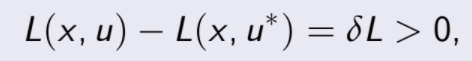
por lo que
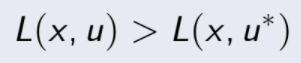
pero esto es una contradicción con el hecho de que u* es un máximo, por lo que
![]()
|