|
#Ejemplo de Sistema Lineal
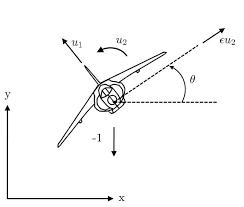
#Para ilustrar el uso del paquete, presentamos un ejemplo del diseño de un arquitectura de # control de bucle interior/exterior para el despegue y aterrizaje vertical planar (PVTOL) #ejemplo en FBS2e.
import control as ct
import matplotlib.pyplot as plt
import numpy as np
# Parámetros del Sistema
m = 4 # Masa de la aeronave
J = 0.0475 # Inercia alrededor del eje de cabeceo
r = 0.25 # Distancia al centro de fuerza
g = 9.8 # Constante gravitacional
c = 0.05 # Factor de amortiguamiento (estimado)
# Funciones de transferencia para dinámica
Pi = ct.tf([r], [J, 0, 0]) # Bucle interior (rollo)
Po = ct.tf([1], [m, c, 0]) # Bucle exterior (posn)
# Diseño de control de bucle interno
#Controlador de la dinámica de tono: el objetivo es
#para tener una respuesta rápida para que podamos usar esto
#como un proceso simplificado para la dinámica lateral
#Diseñe un controlador principal simple para el sistema
k_i, a_i, b_i = 200, 2, 50
Ci = k_i * ct.tf([1, a_i], [1, b_i])
Li = Pi * Ci
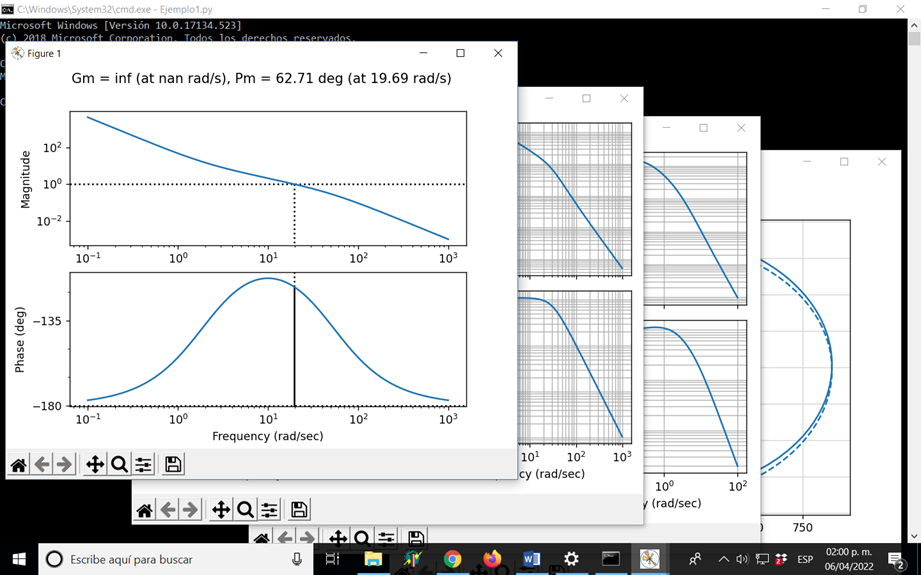
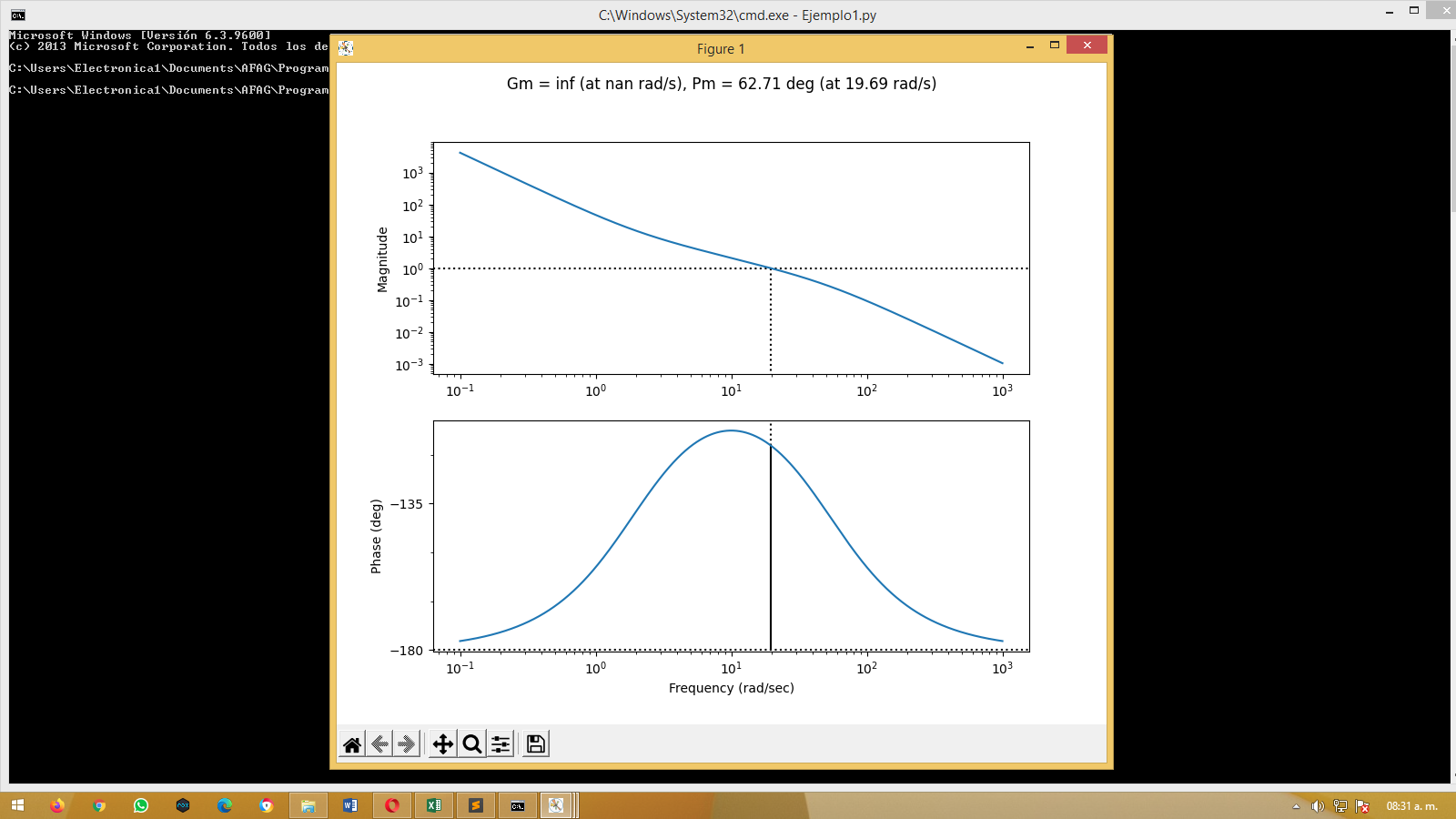
# Loop transfer function Bode plot, with margins
plt.figure(); ct.bode_plot(Li, margins=True)
plt.savefig('pvtol-inner-ltf.pdf')
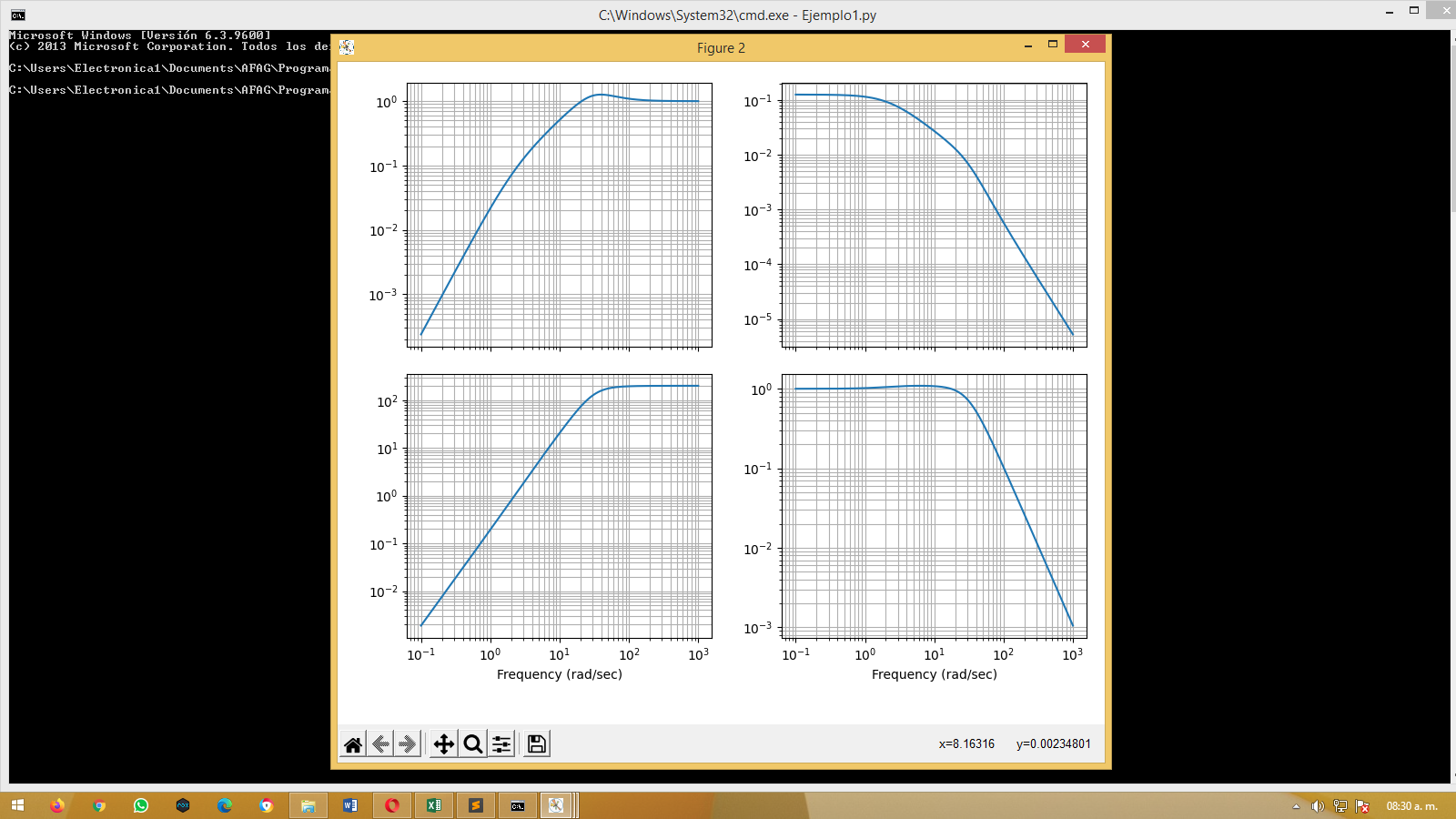
# Make sure inner loop specification is met
plt.figure(); ct.gangof4_plot(Pi, Ci)
plt.savefig('pvtol-gangof4.pdf')
# Diseño del sistema de control lateral (compensador de plomo)
a_o, b_o, k_o = 0.3, 10, 2
Co = -k_o * ct.tf([1, a_o], [1, b_o])
Lo = -m * g * Po * Co
# Calcule la función de transferencia de bucle de bucle exterior real
L = Co * Pi * Po
# Calcular los márgenes de estabilidad
gm, pm, wgc, wpc = ct.margin(L)
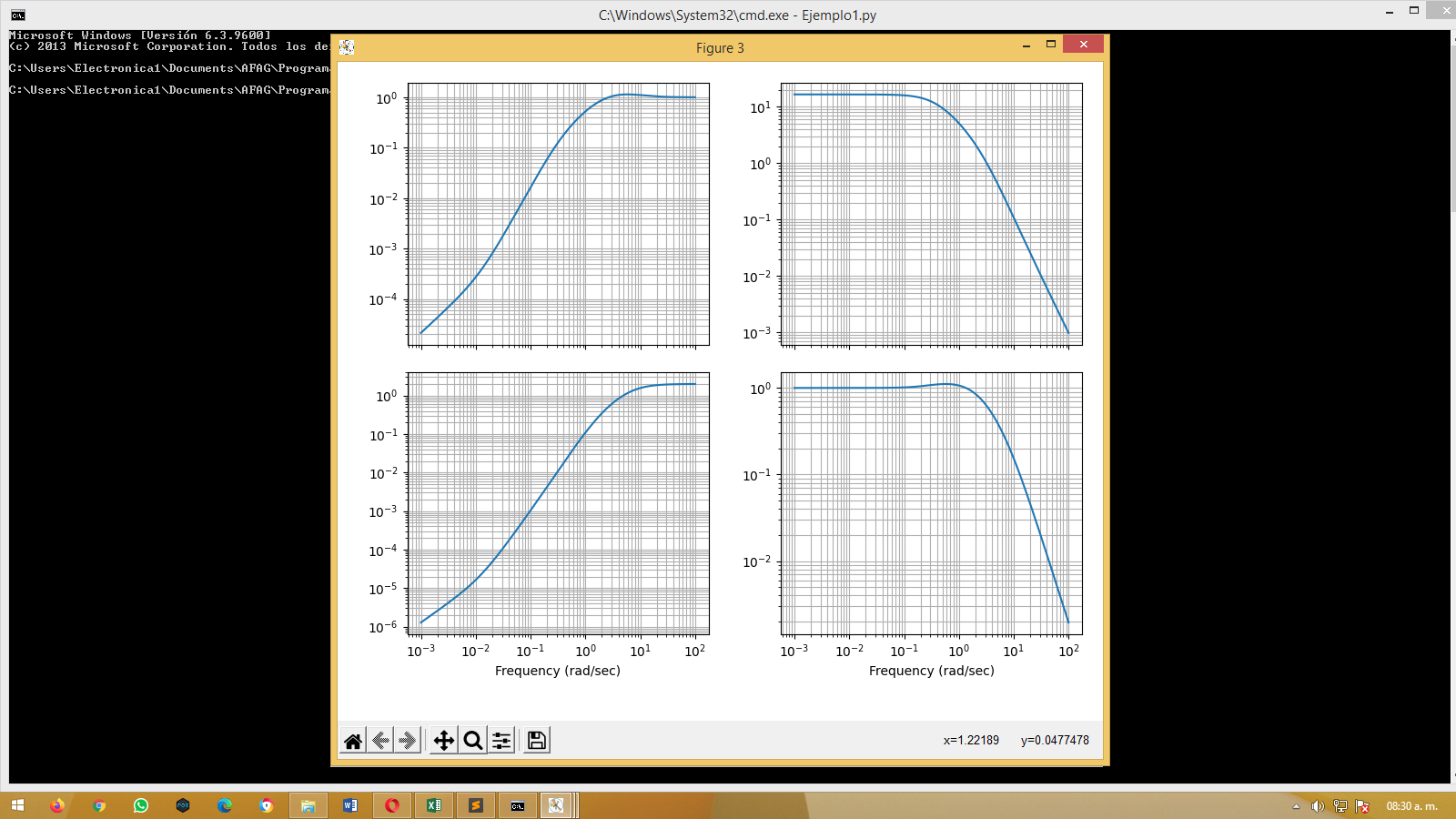
# Verifique que se cumpla la especificación
plt.figure(); ct.gangof4_plot(-m * g * Po, Co)
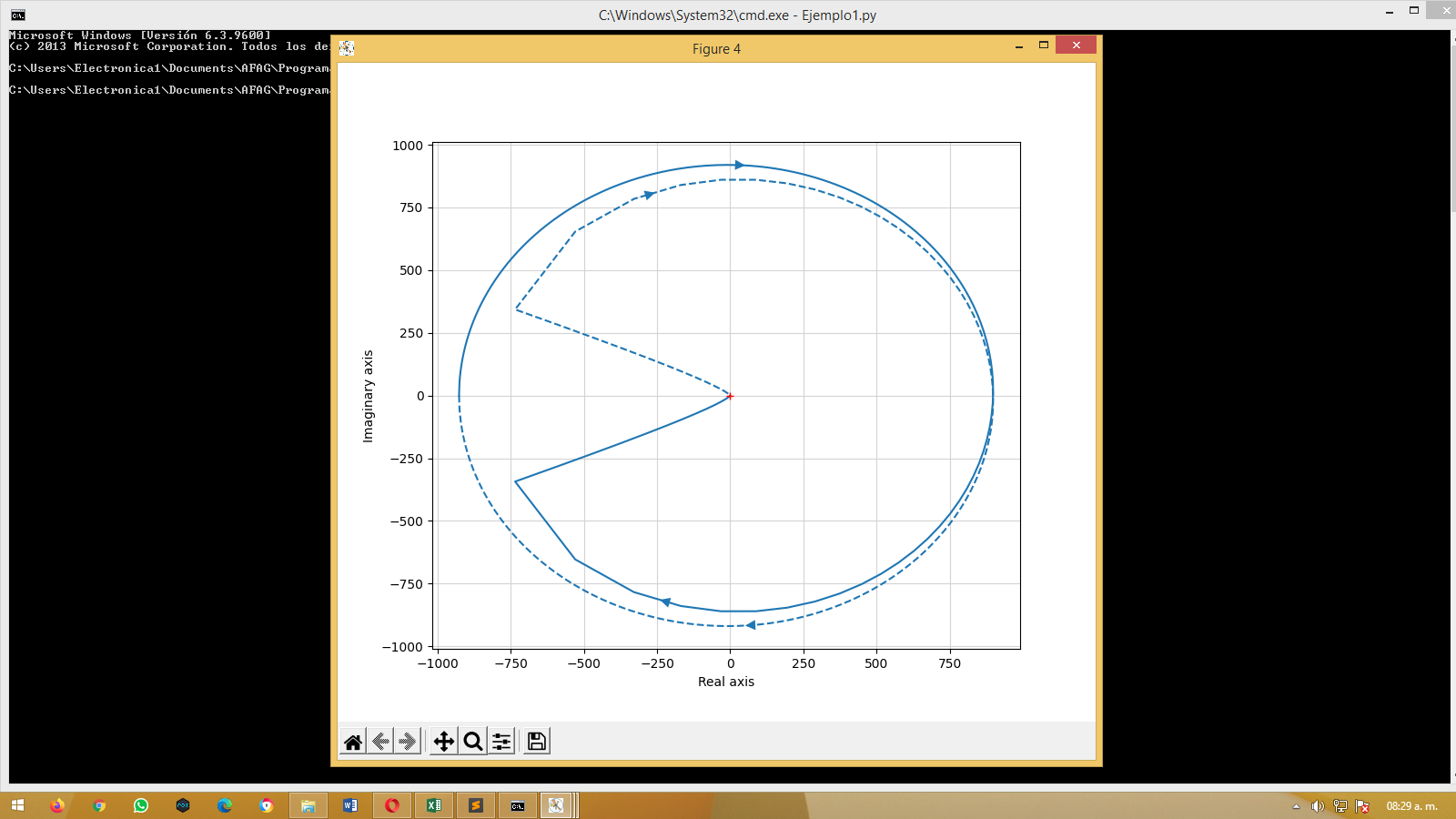
# Diagrama de Nyquist para un diseño completo
plt.figure(); ct.nyquist_plot(L)
plt.savefig('pvtol-nyquist.pdf')
# problema
# Step response
plt.savefig('pvtol-step.pdf')
plt.show()
|